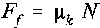


Objectives:
Develop and apply a design tool using Working Model to evaluate the effect of friction in the
design of part of a conveyer system.
Instructional Objectives
Application of Newton's Second Law to a practical engineering problem. Learning several
Working Model features including modeling of friction, defining controls, defining friction, contact
and gravitational force vectors, defining frames of reference, use of grid snap and rotation tools.
Background:
A classical dynamics textbook problem involves the acceleration or deceleration of blocks
sliding down planes with friction between the block and the plane. One application of this type of
analysis is in conveyer systems where friction is used to control the velocity of components sliding
down inclined planes. When high velocities are desired, rollers are used which can be modeled as
planes with zero friction. If the velocity is to remain low or if the component is to come to a stop
during sliding, the designer can increase the friction coefficient to obtain the desired results.
In this assignment, a Working Model simulation will be developed which will allow a designer to easily vary the kinetic friction coefficient. Recall that during sliding, the frictional force generated is proportional to the normal force between the block and the inclined plane
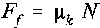
where µk is the coefficient of kinetic friction. According to Newton's Second Law, if we define the x-direction to be parallel to the inclined plane and the y- direction to be normal to the plane, with ay=0
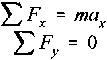
With the free body diagram
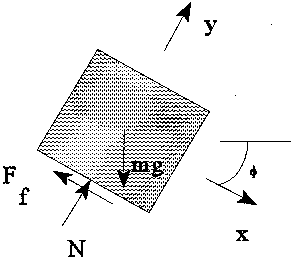
the equations of motion become
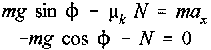
Solving for the acceleration in the x-direction yields
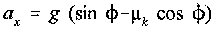
Note that µk=tan Ø yields the acceleration ax=0. Values of µk > tan Ø result in deceleration of the box and values of µk < tan Ø result in acceleration of the box.
In this exercise, the objective is apply this analysis to an inclined plane at the end of a conveyer belt as shown below. The goal is to bring the box to a full stop near the end of the inclined plane. Furthermore, we'd like to minimize the time required to travel from the top of the plane to the final resting point. To achieve this result, we can vary the friction coefficient along the length of the inclined plane.
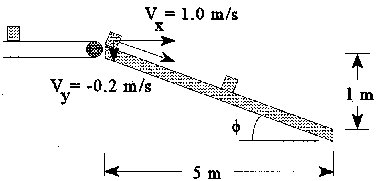
Your assignment is to create a Working Model simulation of the inclined plane with up to five segments of equal length. The box must come to a full stop somewhere in the final (fifth) segment of the inclined plane. The coefficient of kinetic friction between the box and each segment can vary between 0 and 0.25. The coefficient of static friction is assumed to be greater than 0.25, yielding no sliding once the box comes to a full stop. Hint: to minimize the time required, allow the box to accelerate near the top of the inclined plane and then decelerate to a stop near the bottom. Do not allow the box to slide off the end of the inclined plane.
To be turned in: