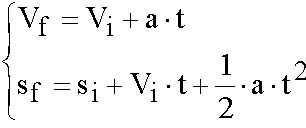Raccolta casi Working Model, visualNastran & SimWise - Studio termomeccanico di un freno a tamburo per veicoli pesanti

Contatto Editoriale:
Paolo Lista,
Lista Studio srl®
Borgo Belvigo 33, 36016 Thiene Vi ITALY
tel/fax 0445,372479 o info@lista.it
STUDIO TERMOMECCANICO
DI UN FRENO A TAMBURO
PER VEICOLI PESANTI
D. Giangreco, G. Virzì Mariotti*
* = Università degli studi di Palermo; Dipartimento di Meccanica, Viale delle Scienze 90128 Palermo, Italy.
Memoria presentata al XXXV Convegno Nazionale AIAS, 13-16 Settembre 2006, UniversitÓ Politecnica delle Marche, Ancona.
Pubblicata con il permesso del prof. Gabriele Virzì Mariotti.
Sommario
Scopo di questo lavoro è quello di analizzare il comportamento termomeccanico di un freno a tamburo Rockwell di tipo Simplex a ganasce flottanti da 410×200 mm di ultima generazione, montato sull’asse posteriore del veicolo pesante Iveco Stralis Executive Space. Lo studio è stato condotto attraverso simulazione numerica, facendo uso del software MSC.visualNastran. La modellazione è stata suddivisa in due fasi, la prima per lo studio del comportamento termico e l’altra per lo studio di quello meccanico, sviluppando così un modello funzionale in grado di prevedere il comportamento del freno nelle diverse condizioni. Lo studio è stato eseguito considerando la variazione di alcuni parametri strutturali con la temperatura, quali il calore specifico, la conduttività interna ed il modulo elastico del materiale del tamburo. Il risultato principale dell’analisi è il calcolo di tensioni e deformazioni nel tamburo e nei ceppi con il miglioramento strutturale del freno.
Abstract
Purpose of this paper is the analysis of the thermo mechanical behaviour of a Rockwell drum brake of Simplex type with floating shoes 410x200 of the last generation, assembled on the rear axis of the heavy vehicle Iveco Stralis Executive Space. The study was conduced by numerical simulation, using the software MSC Visual Nastran. The modelling was subdivided in two stages, the first for the study of the thermal behaviour and the other for the mechanical one, so developing a functional model fit for foresee the behaviour of the drum brake under several braking conditions. The study is conduced considering the variation of some structural parameters with the temperature, as the specific heat, the internal conductivity and the elastic modulus of the drum material. The principal result of the analysis is the stress and strain calculation in the drum and in the shoes, with the aim of the brake structural improving.
Parole chiave: Freni a tamburo, elementi finiti, simulazione dinamica, Analisi termomeccanica
1. INTRODUZIONE
Scopo di questo lavoro è quello di analizzare il comportamento termomeccanico di un freno a tamburo montato sull’asse posteriore del veicolo pesante Iveco Stralis Executive Space. Si tratta in particolare di un freno a tamburo Rockwell di tipo Simplex a ganasce flottanti da 410×200 mm di ultima generazione. Lo studio è effettuato tramite simulazione virtuale per mezzo del software di simulazione dinamica MSC.visualNastran, che usa il metodo degli elementi finiti e consente di affrontare numerosi problemi di natura progettuale, garantendo risultati di una certa attendibilità. Esso permette, fra l’altro, lo studio del transitorio termico e delle non linearità a causa del diverso comportamento al variare della temperatura. Il metodo di risoluzione adottato dal programma è il “metodo degli spostamenti nodali” che permette di risolvere, tramite alcune ipotesi aggiuntive, le strutture continue che vengono discretizzate in elementi legati fra di loro.
La modellazione è stata suddivisa in due fasi, la prima per lo studio del comportamento termico e l’altra per lo studio di quello meccanico; con il modello termico si calcola la temperatura del tamburo, con quello meccanico si esegue un’analisi dinamica e statica del freno, calcolando tensioni e deformazioni.
Il modello proposto è utile in sede di progettazione perché favorisce la scelta dei materiali del freno a tamburo, con l’obiettivo è ottenere un freno, in grado di generare un’azione frenante compatibile con le prestazioni richieste dall’autoveicolo, ma di massa limitata al fine di migliorare le sue prestazioni su strada in termini di confort. Ciò si deve conciliare con l’esigenza di evitare un eccessivo riscaldamento del freno stesso, che potrebbe comprometterne l’efficacia; occorre così trovare il giusto compromesso fra due opposte esigenze la cui scelta è agevolata dal modello di simulazione.
In effetti, il particolare problema trattato non è frequente in bibliografia; i lavori sui freni a tamburo riguardano principalmente le applicazioni della teoria di Romiti o di altre teorie e l’uso di alcuni rapporti caratteristici quali il rapporto di efficacia o “brake factor” [1] [2] [3] [10] [11] [17] [18][19][20][21][22]. In particolare le formulazioni teoriche danno risultati affetti da errore perché si trascura la deformabilità delle parti a contatto, che influisce in modo determinante sulla distribuzione delle pressioni; esse conducono a risultati differenti l’una dall’altra ma comunque discordanti con quelli ottenibili con la simulazione numerica [4] [5] [6]. In questo lavoro si è quindi rinunciato al confronto con i risultati ottenibili per via teorica, ritenendo più affidabili i risultati della simulazione per i motivi sopra enunciati.
Le tensioni agenti sul freno a tamburo sono essenzialmente di tipo meccanico, cioè dovute allo sforzo esercitato per conseguire la frenatura e di tipo termico, cioè in seguito all’aumento di temperatura si destano nel tamburo e nelle varie parti del freno tensioni termiche che stressano pesantemente le parti a contatto specialmente nel transitorio. Il calore sviluppato all’interfaccia ganascia tamburo produce un flusso termico che può essere determinato facilmente con considerazioni energetiche, ma meno immediata è la determinazione del modo con il quale detto flusso termico si ripartisce fra le superfici a contatto. Al fine di evitare errori di valutazione in questo lavoro si è fatta l’ipotesi che il flusso termico generato sia assorbito dal solo tamburo, il che non è molto lontano dalla realtà e va a vantaggio della sicurezza. I problemi che si incontrano nella determinazione delle temperature sono del tutto simili a quelli che si incontrano nei freni a disco e che sono stati affrontati in [7], mentre in [8] e [9] sono stati considerate anche le variazioni di alcuni parametri strutturali con la temperatura; infine in [9] la particolare ipotesi fatta per la ripartizione del flusso termico fra pattino e disco ha avuto un conforto sperimentale più che soddisfacente. Infine in questo lavoro il coefficiente di adduzione [12] [23] è stato considerato una funzione della velocità del veicolo

Figura 1: Fotografia dei componenti del freno Rockwell Simplex a ganasce flottanti.
2. COSTRUZIONE E FUNZIONALITÀ DEL FRENO
La fig. 1 mostra il freno Rockwell a ganasce flottanti (410x200) esploso in tutti i suoi componenti. Le superfici frenanti sono costituite da due elementi frenanti per ogni ganascia aventi un’apertura angolare di 60°. Di notevole interesse è il sistema di autoregistrazione i cui componenti sono mostrati nella parte alta della fig. 1, costituito da una coppia vite-madrevite, la cui regolazione automatica si effettua in modo tale che il ritorno della ganascia alla fine della frenata sia sempre la stessa quantità, indipendentemente dallo spostamento necessario per ottenere il contatto. Ciò compensa il maggior spostamento necessario per l’usura della ganascia. Altri elementi di notevole interesse sono i perni di ancoraggio, mostrati nella figura 1 in basso, e i due perni di registro; essi presentano un incasso di sagomatura diversa l’uno dall’altro che, unitamente al fatto che il freno è flottante, fa sì che le due ganasce avvolgente e svolgente presentino brake factor quasi uguali.
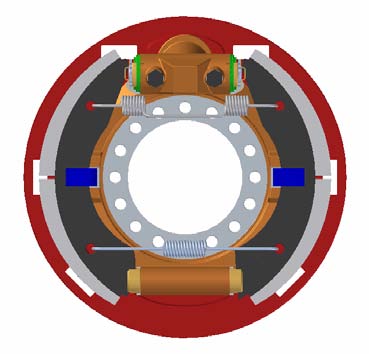

Figura 2 Immagine CAD del gruppo frenante.
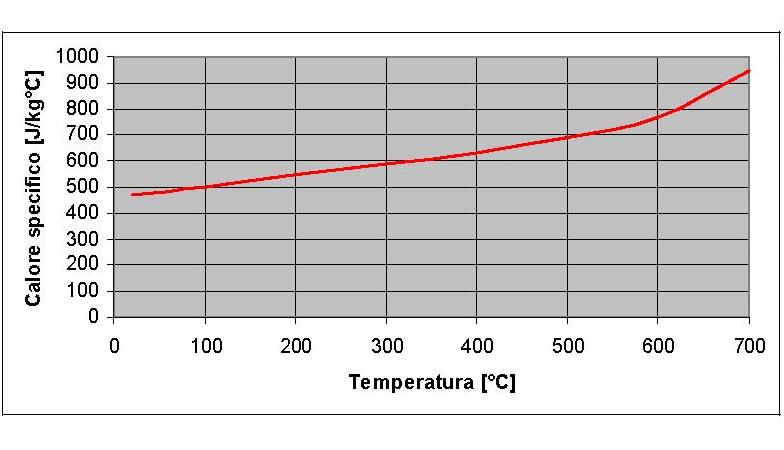
Figura 3: Calore specifico della ghisa
Per mezzo di un programma CAD si sono realizzati i modelli di tutte le parti del freno e dell’assemblaggio di tali parti. La fig. 2 mostra il complessivo composto da tutti i particolari che è stato poi importato in MSC.Visual Nastran per le successive elaborazioni. Si nota fra l’altro che il tamburo presenta un incremento dello spessore nella parte prospiciente il parapolvere e la piastra di supporto a causa della necessità di limitare la deformazione a campana e durante la frenatura.
2.1 Materiali
La tabella 1 riporta i materiali utilizzati per la costruzione del freno e le loro principali caratteristiche [13-16]. In particolare le caratteristiche della ghisa sono date a temperatura ambiente. Nelle figure 3, 4 e 5 sono riportati rispettivamente i valori del calore specifico, della conduttività termica, del modulo di Young della ghisa GH190 al variare della temperatura [8] [9].
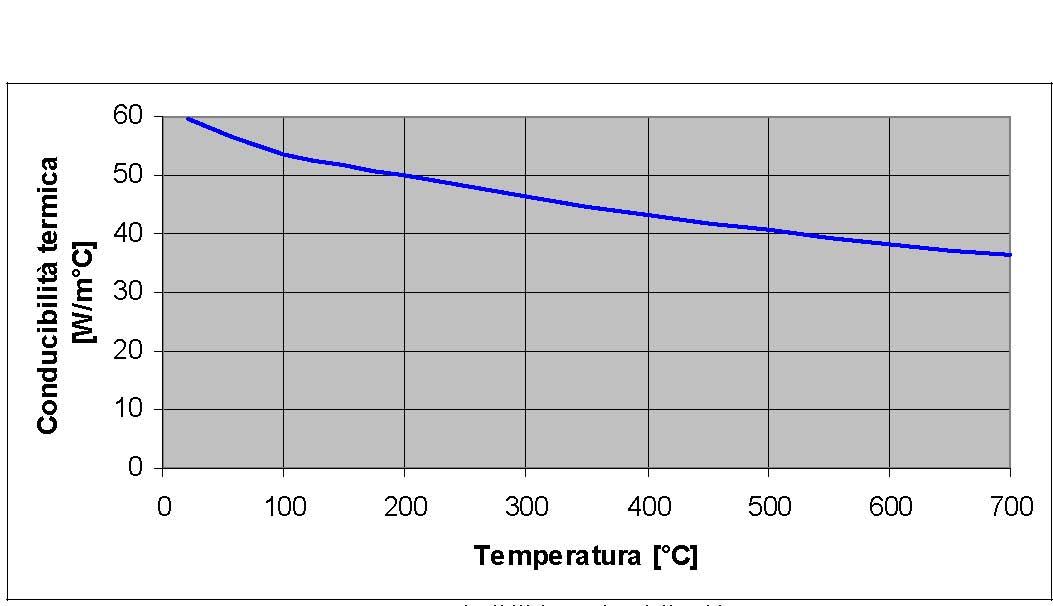
Figura 4: Conducibilità termica della ghisa.
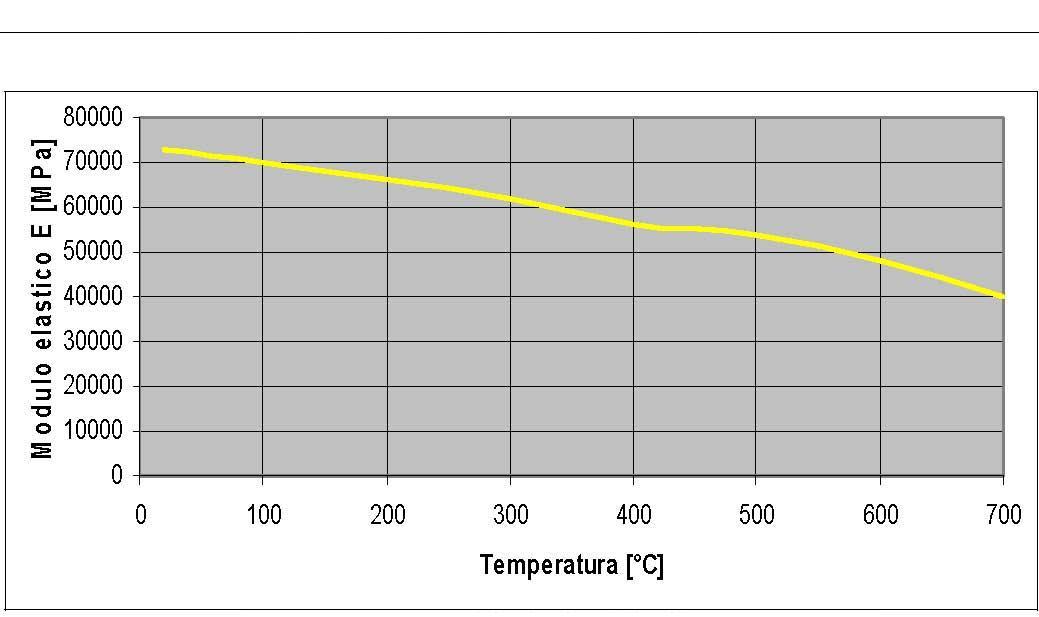
Figura 5: Modulo elastico della ghisa.
Tab. 1 – Principali caratteristiche dei materiali usati per la costruzione del freno
| Ghisa GH190 per il tamburo (T= 20°C) | Materiale d’attrito per le guarnizioni frenanti | Acciaio per le ganasce |
Modulo elastico | E=73000 MPa | E=372 MPa | E=206000 MPa |
Coefficiente di Poisson | ν=0,27 | ν=0,25 | ν=0,3 |
Densità | ρ=7.2 kg/dm3 |
|
|
Calore specifico | cp=469J/(kg°C) |
|
|
Conduttività termica | K=59,7 W/(m°C) |
|
|
Tensione di rottura a trazione | σrt=250 MPa |
| 448 MPa |
Tensione di rottura a compressione | σrc=750 MPa |
| 310 MPa |
Coefficiente di dilatazione termica lineare | α=9,67 10-7 1/°C |
|
|
Coefficiente di attrito |
|
|
|
3. CALCOLI DI FRENATURA
Il veicolo ha una massa totale a terra m = 18000 kg e viaggia su strada piana; la resistenza aerodinamica e le azioni di disturbo dovute al vento sono trascurate. Lo spazio d’arresto in condizioni di aderenza è pari a 95,2 m in un tempo di 6,23 s se la velocità iniziale è pari a 110 km/h e se la decelerazione media è pari a 0,5g. Supponendo inoltre un’uguale ripartizione della frenata sulle ruote dello stesso asse, il momento frenante applicato al tamburo, è pari a:
| (1) |
Se durante la frenata sull’asse posteriore grava il 30% del carico totale, se il coefficiente di aderenza tra ruota e terreno è fx = 0,85 e il coefficiente di inerzia è ka = 1,1 per l’effetto inerziale delle masse rotanti,, la forza tangenziale Ft che agisce all’interfaccia ruota-terreno è pari a:
| (2) |
Poiché gli pneumatici del veicolo hanno una circonferenza di rotolamento C0 = 3400 mm, il momento frenante è pari a:
| (3) |
Il flusso di calore è calcolato in base alla variazione di energia cinetica necessaria per arrestare il veicolo che viaggia a 110 km/h ed è pari a:
| (4) |
Il lavoro frenante, equivalente al calore sviluppato sul tamburo durante la frenata, è pari a:
| (5) |
Tale lavoro è trasformato interamente in calore e dissipato nell’ambiente esterno, essendo esigua la percentuale di calore assorbita dalle guarnizioni frenanti e dagli altri organi in contatto con il tamburo. Il flusso termico entrante nel tamburo durante la frenata è pari a:
| (6) |
3.1 Carico termico e meccanico
L’obiettivo della simulazione è determinare il campo termico, lo stato di tensione e di deformazione nel tamburo nei vari istanti di frenata. Per far questo occorre fissare le modalità di scambio termico, in termini di calore generato per attrito e calore dissipato. Il coefficiente convettivo [12] è strettamente dipendente dalle condizioni al contorno (geometria del tamburo, posizione del tamburo all’interno del vano ruota, aerodinamica del veicolo ecc.) e può essere assunto [23] pari a:
| (7) |
dove D è il diametro esterno del tamburo (410 mm) ed Re il numero di Reynolds. Ad una temperatura di 20 °C la conducibilità termica, la densità e la viscosità dell’aria sono pari rispettivamente a:
| (9) |
La figura 6 mostra i valori del coefficiente di scambio convettivo espresso dalla (7) in funzione della velocità del veicolo. Il calore trasmesso per irraggiamento è proporzionale alla quarta potenza della temperatura:
| (10) |
essendo ε l’emissività, A l’area della superficie, ![]() la costante di Stefan-Boltzmann e Ts e Tcirc le temperature della superficie e dell’ambiente circostante. Detta quantità di calore è stata trascurata perché di entità inferiore rispetto a quella trasmessa per convezione; inoltre in letteratura non sono stati reperiti dati certi sull’emissività per il caso in oggetto.
la costante di Stefan-Boltzmann e Ts e Tcirc le temperature della superficie e dell’ambiente circostante. Detta quantità di calore è stata trascurata perché di entità inferiore rispetto a quella trasmessa per convezione; inoltre in letteratura non sono stati reperiti dati certi sull’emissività per il caso in oggetto.
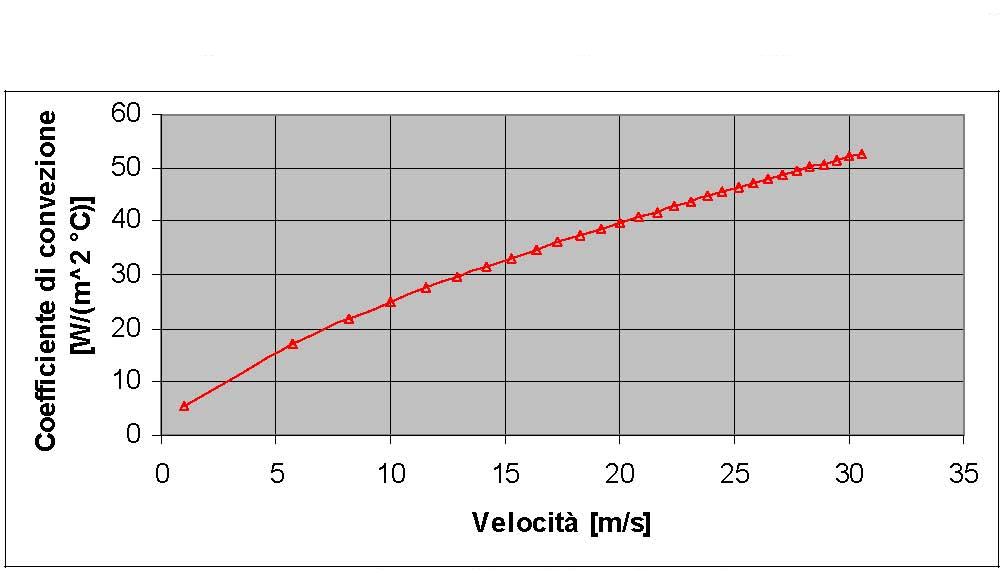
Figura 6: Andamento del coefficiente di convezione.
Le superfici non interessate dal flusso termico entrante disperdono calore verso l’esterno; flusso termico e convezione sono applicati contemporaneamente per tutta la durata della frenata. Il software richiede come dato di input il flusso termico specifico, cioè il calore entrante per unità di tempo e della superficie laterale interna del tamburo durante la frenata, che è pari a:
| (11) |
dove Ri è il raggio interno del tamburo e B (200 mm) la larghezza delle guarnizioni frenanti.
Nella zona di contatto tamburo - guarnizioni frenanti si sviluppano pressione meccanica e calore per attrito che è poi trasmesso dallo stesso tamburo, per tutto il tempo in cui non è sottoposto alle pressioni di contatto, all’ambiente circostante. L’aspetto termico del problema è rappresentabile come una sorgente di calore in movimento su una superficie cilindrica, in una successione ciclica di fasi di riscaldamento e di raffreddamento. Un punto su una circonferenza della superficie cilindrica dove è applicata la pressione delle guarnizioni frenanti, subisce “oscillazioni” di temperatura con periodicità variabile a causa della riduzione della velocità del veicolo durante la frenata. Ciò può indurre fenomeni di instabilità termoelastica che sono oggetto di studio da parte di molti ricercatori. Poiché la decelerazione è costante, la variazione di energia cinetica ed il calore sviluppato sono costanti per ogni giro. Ciò può essere dimostrato partendo dal seguente sistema di equazioni del moto:
| (12) |
dove Vf, Vi, a, sf, si e t sono rispettivamente la velocità finale, la velocità iniziale, la decelerazione, lo spazio finale, lo spazio iniziale ed il tempo. Eliminando il tempo fra le due formule (12) dopo alcuni passaggi si ottiene la seguente relazione:
| (13) |
O, ciò che è lo stesso, la variazione di energia cinetica in un giro è costante assieme alla quantità di calore generata, perché la quantità sf - si in un giro è pari alla circonferenza di rotolamento C0.
4. SIMULAZIONE TERMICA
Si ipotizza di suddividere il tamburo in sei settori ciascuno di 60° (apertura angolare di una superficie frenante), e, considerando un sistema di riferimento solidale con il tamburo, che la guarnizione si muova con velocità costante nell’arco di un giro. Il tempo impiegato dalla guarnizione per scorrere lungo la superficie del tamburo aumenta tra il giro precedente ed il giro successivo, ed il suo valore può essere calcolato, note che siano la velocità iniziale e finale in un giro. I valori di tempo per giro diviso sei danno il tempo medio che una guarnizione impiega per percorrere un settore di 60°:
| (14) |
Il calore sviluppato per giro da parte di una sola guarnizione frenante è dato da:
| (15) |
dove N è il numero di giri che compie il tamburo pari a Sf (spazio totale di frenatura) diviso C0 (circonferenza di rotolamento del pneumatico). Il flusso termico specifico entrante per giro e per una guarnizione avente apertura angolare 60° risulta:
| (16) |
La figura 7 mostra gli andamenti della velocità iniziale e finale e del tempo medio che impiega una guarnizione a percorrere un settore di 60° in funzione del numero di giri della ruota in frenatura.
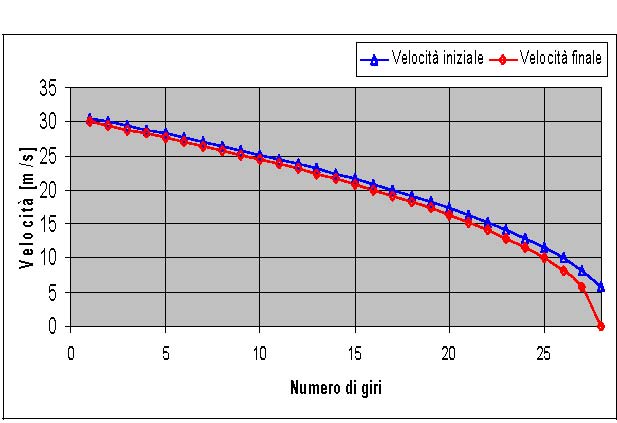
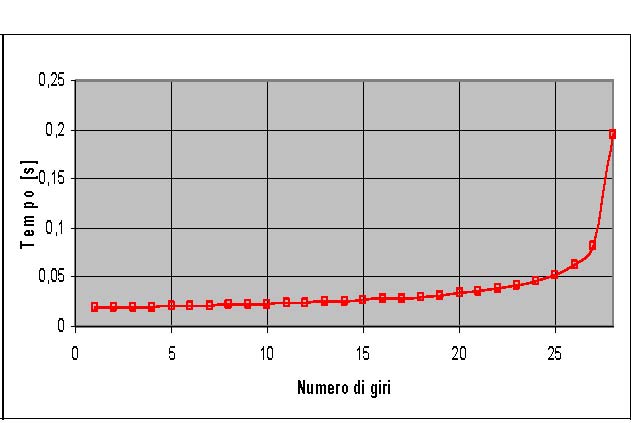
Figura 7: Velocità per giro (a sinistra) e tempo medio per percorrere un settore di 60° (a destra).
La figura 8 mostra le superfici di scambio termico, alle quali è stato applicato il coefficiente di convezione e quelle alla quali è stato applicato il flusso termico specifico. Rispetto ad un osservatore solidale con il tamburo il flusso termico entrante si manifesta con andamento pulsatorio per un tempo pari al tempo che il tamburo impiega a percorrere il settore di 60° corrispondente alla larghezza di una guarnizione, sovrapponendo i contributi delle quattro guarnizioni. La figura 9 riporta la migliore mesh ottenuta caratterizzata da 512071 elementi e 758233 nodi e il risultato ottenuto per la temperatura del tamburo al variare della velocità:
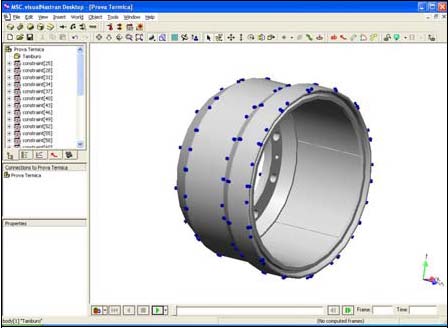
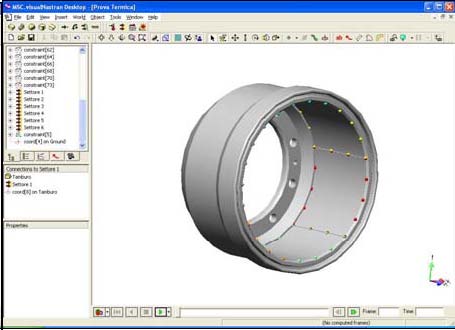
Figura 8: Superfici di scambio convettivo del tamburo (a sinistra) e quelle soggette a flusso termico specifico (a destra).
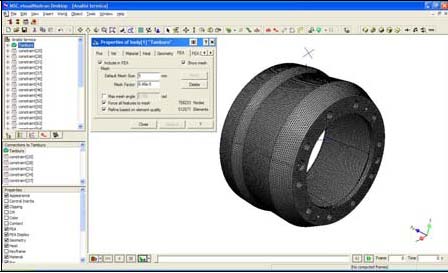
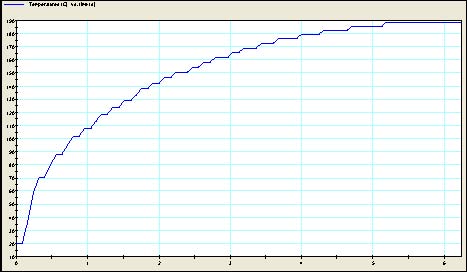
Figura 9: Mesh del tamburo (a sinistra) e temperatura del tamburo in funzione del tempo (a destra)
Si nota che la temperatura nel tamburo assume valori via via crescenti nel corso della frenata, sino ad un valore massimo pari a circa 190°C. Per le condizioni di frenatura ipotizzate il valore non è molto alto, potendosi pensare che la temperatura massima raggiunga valori maggiori nel caso di frenata di emergenza con decelerazioni più sostenute. Il campo termico che si desta all’interno del tamburo nei vari istanti di frenata viene utilizzato come dato di input per l’analisi meccanica del modello.
5. SIMULAZIONE MECCANICA
La figura 10 mostra le tensioni di Von Mises nel tamburo e la deformata a causa della sollecitazione termica e meccanica. Il tamburo, oltre a presentare la classica deformazione a campana, presenta anche una certa ovalizzazione dovuta all’azione delle ganasce; tale deformazione ovviamente non muta di posizione al variare della rotazione ed è amplificata di 162 volte in fig. 10. I valori delle tensioni tuttavia non sono tali da compromettere la resistenza della parte, si arriva infatti ad un valore di tensione di Von Mises di 216 MPa, contro i 750 MPa della resistenza a compressione, dato che le tensioni di origine termica sono di compressione (la superficie interna si trova a temperatura maggiore di quella esterna) e comunque preponderanti rispetto a quelle di trazione. La figura 11 mostra la mesh e la mappa tensionale di Von Mises per la ganascia e per la guarnizione. Anche in questo caso i valori di picco (297 MPa) non sono tali da compromettere la resistenza del materiale delle ganasce, avente un resistenza a trazione ben maggiore. Si nota ancora che la guarnizione superiore della ganascia avvolgente è più sollecitata di quella inferiore; anche in questo caso i valori delle tensioni non sono tali da comprometterne la resistenza, a parte ovviamente il danneggiamento per usura.

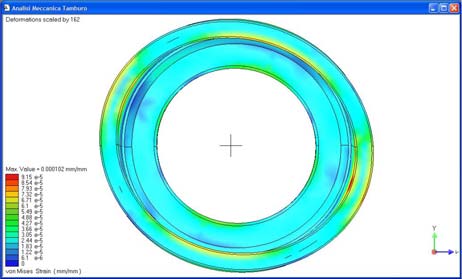
Figura 10: Tensioni di Von Mises (a sinistra) e deformata del tamburo (a destra)
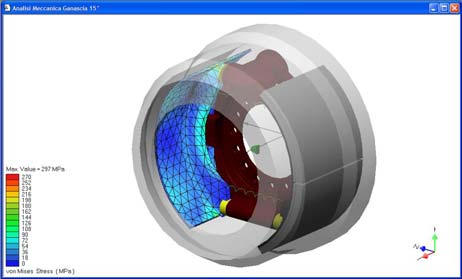
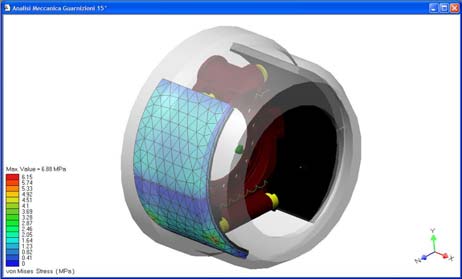
Figura 11: Mesh e tensioni di Von Mises della ganascia avvolgente (a sinistra) e della guarnizione (a destra).
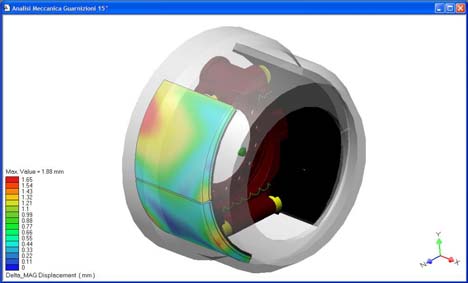
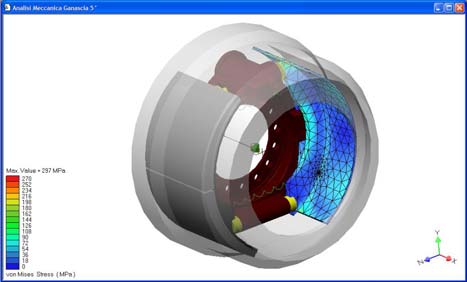
Figura 12: Spostamenti della guarnizione avvolgente (a sinistra).
Mesh della ganascia svolgente e mappa tensionale di Von Mises (a destra).
6. CONCLUSIONI
La diversa geometria dei perni d’ancoraggio di questo tipo di freno dà alle ganasce un Brake Factor quasi uguale. Le ganasce quindi esplicano sul tamburo uno stesso momento frenante, garantendo migliori prestazioni ed usura dello stesso ordine di grandezza per le diverse guarnizioni frenanti.
Dall’analisi termica si è ricavato che i valori di tensione ottenuti non causano stress critico per il tamburo che resiste bene a queste sollecitazioni nella prova di stress termomeccanico. È stato possibile riscontrare anche un rilevante aumento delle temperature del tamburo che provoca una deformazione dello stesso. Le deformazioni termiche non compromettono il corretto funzionamento delle parti meccaniche interessate durante la frenata e nessuna parte del tamburo va ad interferire con gli altri organi meccanici circostanti.
Dall’analisi meccanica si è riscontrato, con riferimento al tamburo, che la parte maggiormente sollecitata risulta essere quella costituita dall’anello rivolto verso la parte interna, molto probabilmente lo spessore di tale settore è stato maggiorato, quasi come si trattasse di una cerchiatura, allo scopo di ridurre le tensioni termiche e la conseguente deformazione a campana. Nelle ganasce si è riscontrato, in corrispondenza delle zone in contatto con i perni d’ancoraggio alla flangia freno e con le viti di registro, un elevato valore di tensioni che potrebbe portare a dannose conseguenze. Per ovviare all’inconveniente si potrebbe maggiorare lo spessore della ganascia per conferirle maggiore resistenza; oppure aumentare lo spessore della nervatura centrale per meglio distribuire i carichi, ridisegnando la geometria dei perni d’ancoraggio e aumentando la sede di battuta delle viti di registro, limitatamente alla zona di contatto con le ganasce. Si ritiene che l’abbattimento dei picchi di tensione riscontrati assicuri al freno maggiore affidabilità e sicurezza, evitando possibili anomalie dopo diversi cicli di frenatura.
BIBLIOGRAFIA
[1] G. Virzì Mariotti, Uso dei rapporti caratteristici nel dimensionamento dei freni a ceppi, ATA Ottobre 1989, vol. 42, n. 10.
[2] G. Virzì Mariotti, Effectiveness factors of vehicle brakes, The American society of mechanical engineers; Paper 86-DET-187, Conference, Columbus, Ohio October 5-8, 1986.
[3] G. Virzì Mariotti, Effectiveness factors in drum brakes design, JUMV XIV Conference Science and Motor Vehicles, Belgrade, May 18-19, 1983 paper YU-93605.
[4] J. Todorović, Č. Duboka, Ž. Arsenić, Dissipation of result obtained during brake testing, Mobility and Vehicle Mechanics, vol. 20, n. 1, March 1994.
[5] Ž. Arsenić, J. Todorović, An analysis of pressure interfacial distribution in a drum brake, Mobility and Vehicle Mechanics vol. 23, n. 2, Jun 1997.
[6] A. J. Day, Drum brake interface pressure distributions, IMechE 1991, Proc. Instn Mech, Engrs, prt D: Journal of Automobile Engineering, vol. 205, pp 127-136.
[7] M. Di Carlo Cuttone, G. Virzì Mariotti, Č. Duboka, Influence of pads and cylinders on thermoelastic behaviour of disk brakes, XVIII Science and motor vehicles 2001, Belgrade, 28-30 May 2001, paper YU-01018.
[8] N. Giacalone, G. Virzì Mariotti, Thermoelastic analysis of a disk brake by taking in account the variabilità of some structural parameters, XIX Science and motor vehicles 2003, Belgrade, (Yu), 26-28 May 2003, Paper YU-03014.
[9] Dragan Aleksendrić, Čedomir Duboka, Pier Francesco Gotowicki, Vincenzo Nigrelli, Gabriele Virzì Mariotti - Braking Procedure Analysis Of A Pegs-Wing Ventilated Disk Brake Rotor - Int. J. Vehicle Systems Modelling and Testing, Vol. 1, No 4, 2006
[10] Rudolf Limpert, Brake design and safety, SAE International, 1999.
[11] Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas, Progetto e costruzione di macchine, McGraw-Hill Companies Srl, Milano 2005.
[12] Yunus A. Çengel, Termodinamica e trasmissione del calore, McGraw-Hill Libri Italia Srl., Milano 1998.
[13] M. Teora, Fenomenologia della frenata, ATA n. 11, 1984.
[14] P. Bassignana, E. Gavello, S. Leonti, Analisi termica, termoplastica e meccanica di freni automobilistici, ATA n. 11, 1984.
[15] Braiato, C. Rossi, Sperimentazione su strada degli impianti di frenatura, ATA n. 11, 1984.
[16] G. Belingardi, Esame delle principali caratteristiche dei materiali di attrito utilizzati per freni delle autovetture, ATA n. 11, 1984.
[17] Newcomb & Spurr - Automobile brakes and braking sistems. Chapman and Hall, London 1969.
[18] Guido Bongiovanni, Giovanni Roccati - Freni, Levrotto & Bella, Torino, 1993.
[19] Rosario Scuto, Pietro Leone - Tecnica dell’autoveicolo, Levrotto & Bella, Torino 1967.
[20] F. Buffoni - L’autoveicolo, Ulrico Hoepli, Milano 1965.
[21] Giuseppe Pollone, Il veicolo, Costruzioni automobilistiche, Levrotto & Bella, Torino 1960.
[22] Newcomb & Spurr, Braking of road vehicles, Chapman and Hall, London, 1967.
[23] N. Natarajan, S. Vijayarangan, I. Rajendran - Fabrication, testing and thermal analysis of metal matrix composite brake drum - International Journal of Vehicle Design (IJVD), Special Issue: “Design and Manufacturing of Land Transport Structures using Composite Materials”, July 2006
OTHER 83 DIFFERENT APPLICATIONS !
ALTRI 83 CASI IN SETTORI DIVERSI !