
Contatto Editoriale:
Paolo Lista,
Lista Studio srl®
Borgo Belvigo 33, 36016 Thiene Vi ITALY
tel/fax 0445,372479 o info@lista.it
TODDLER TOPPLING BACKWARDS
Low-level Fall Simulation: Toddler Toppling Backwards
R. J. Reimann, Professor Emeritus of Physics, Boise State University, 11 June 2012 (rev. 7/9/2013)
This simulation was generated using Working Model® software licensed at Boise State University for educational use only.
Situation
Toddlers occasionally topple over and hit their heads on the floor.
They might stumble over something or simply lose balance and lean back too far.
Resulting impacts have potential for grievous injury and even death [1].

An extreme case occurs if the joints are frozen by fear or defiance and the head hits first.
The model predicts an initial vertical impact speed vy = 3.72 m/s. Note that this slightly exceeds vy = square of 2gh = 3.70 m/s predicted by free-fall for the point simply dropping at h = 0.70 m and the acceleration due to gravity g = 9.8 m/s².
Refinements
The following simulation allows flexible joints and other variable parameters to demonstrate one of countless possible scenarios
between the previous rigid extreme and cases where the head does not even hit the floor.
It is intended as a demonstration aid that is more realistic than an artist's conception.
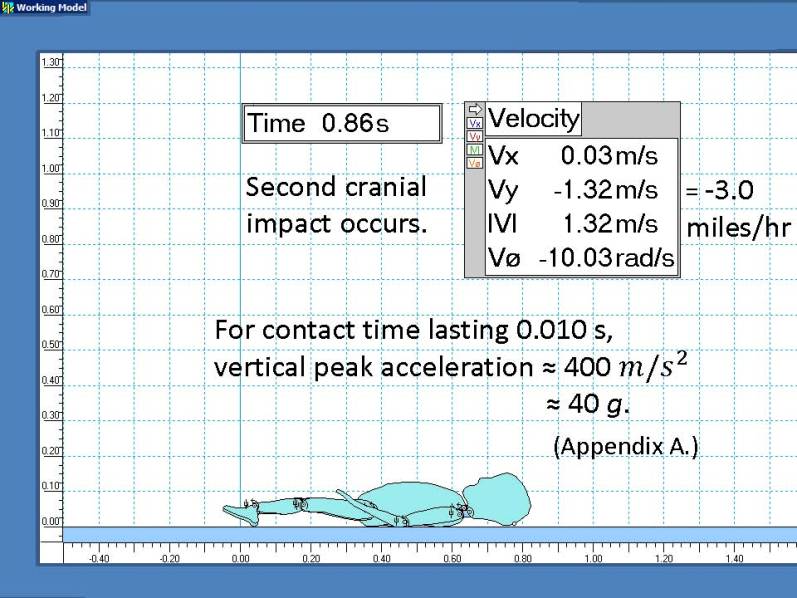
Although the torso lands first, the head is still predicted to hit at vy > 3 m/s or more than 80% of the previous free-fall result.
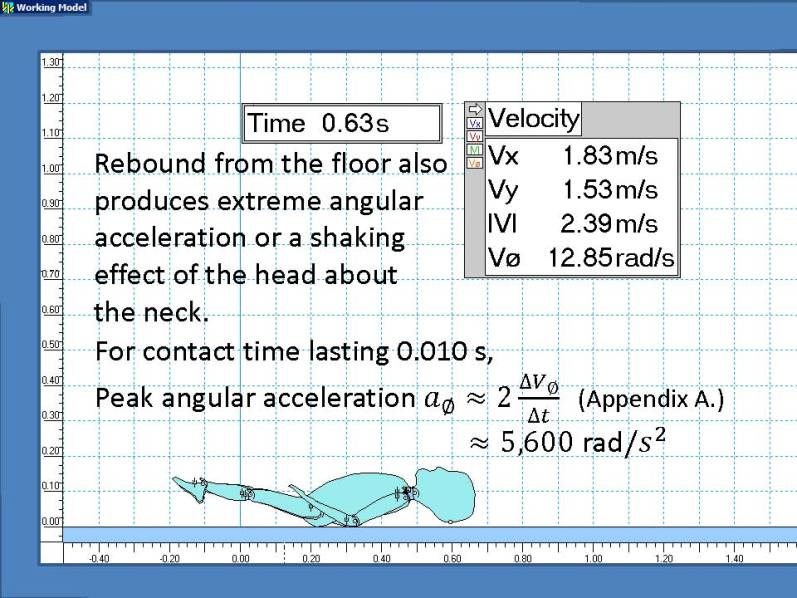
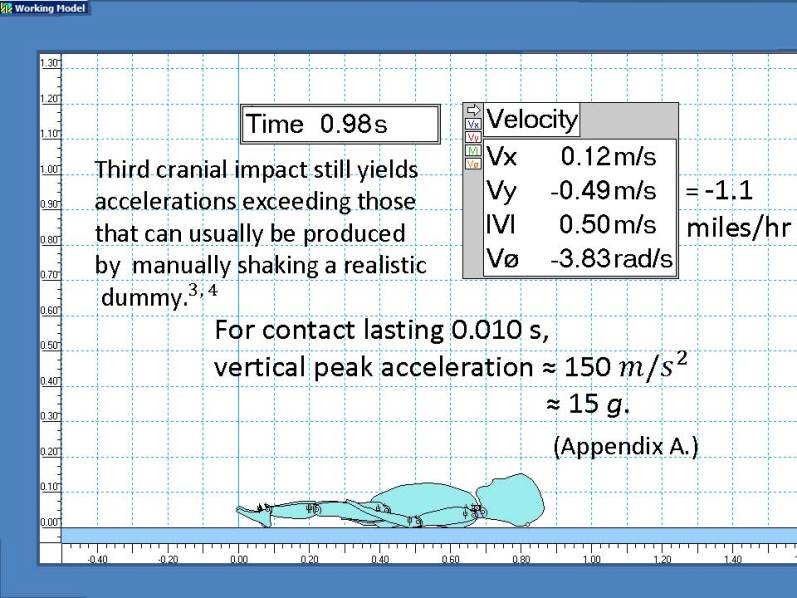
Derived results such as accelerations depend on contact time as explained in Appendix A.
Prediction reliability is limited by the choice of model parameters given in Appendix B (mass distribution, joint approximations, elasticity
and friction).
Any changes to these parameters, initial posture, or rigidity of linked segments may change the outcome significantly.
The simulation is based on average dimensions for an 18-month old child crash-test dummy [2] with a stature of 0.81 m and mass of 11.0 kg, including a 2.6 kg head. More details are given in Appendix B.
Scale dimensions are in meters. Velocities are displayed for the initial cranial impact point.
The integrity of the software was checked by generating accurate predictions for cases with known analytical solutions.
These were free-fall for a ball and toppling a long thin vertical rod about an ideal axis fixed at the bottom.
Other computer simulations, physical models and video analysis are invited for comparison to help evaluate this simulation.
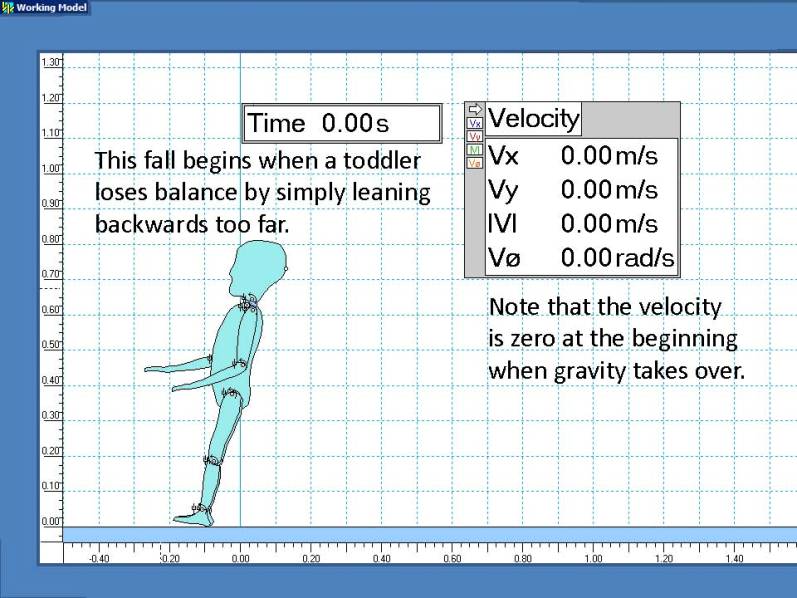
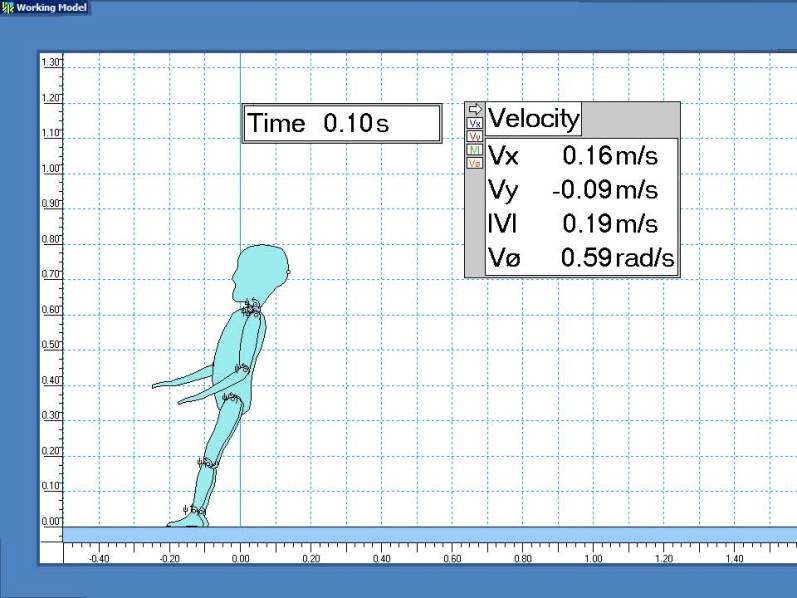
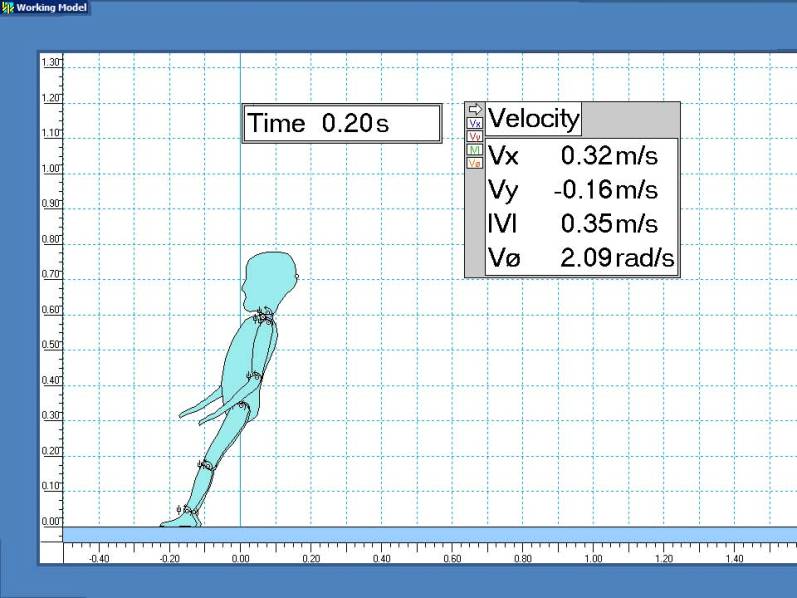
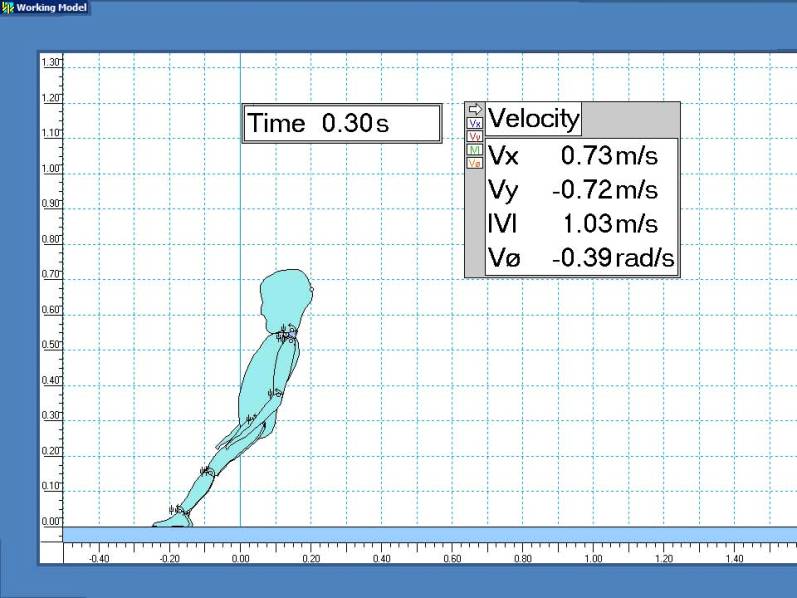
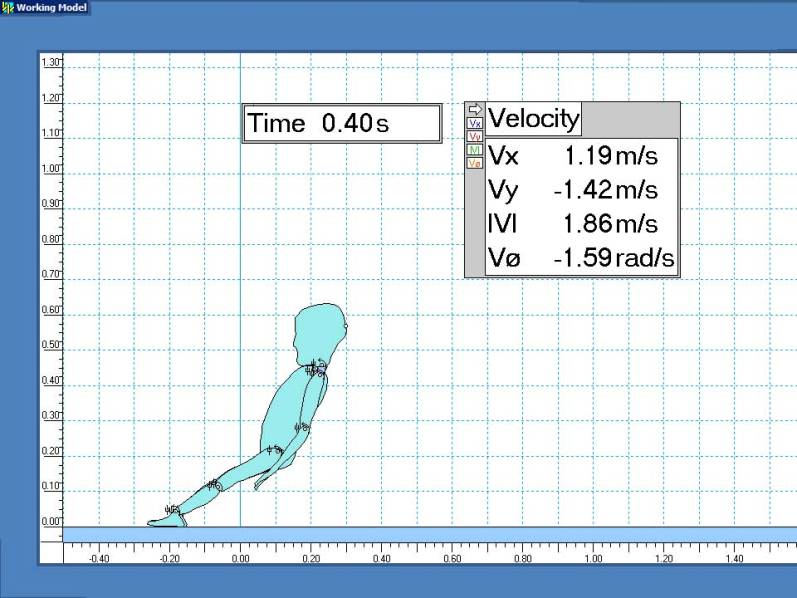
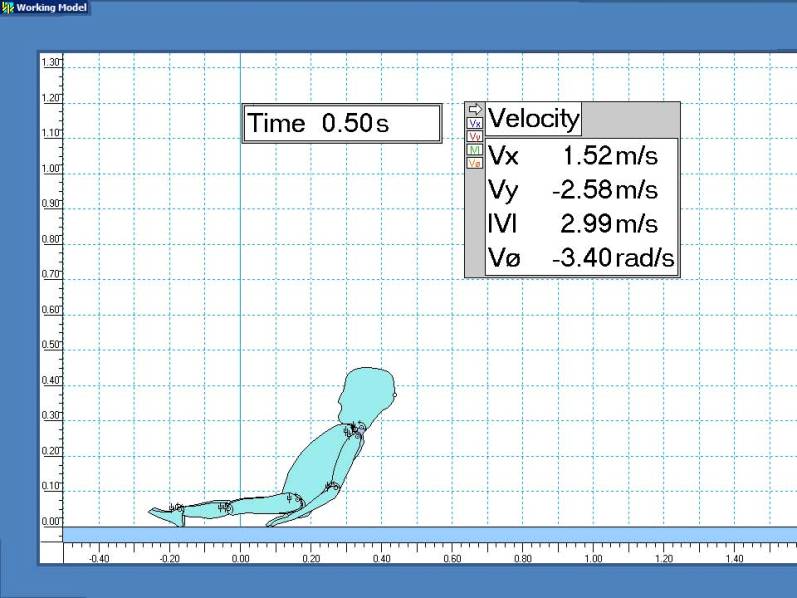
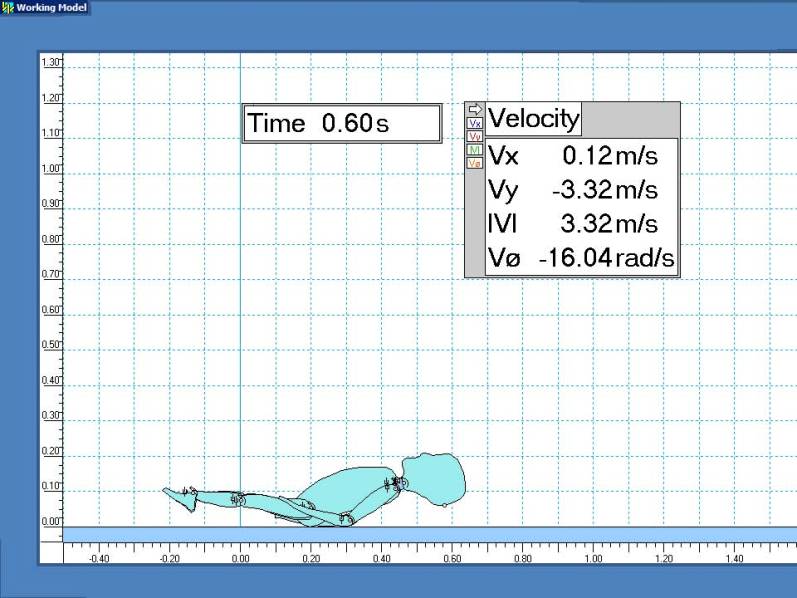
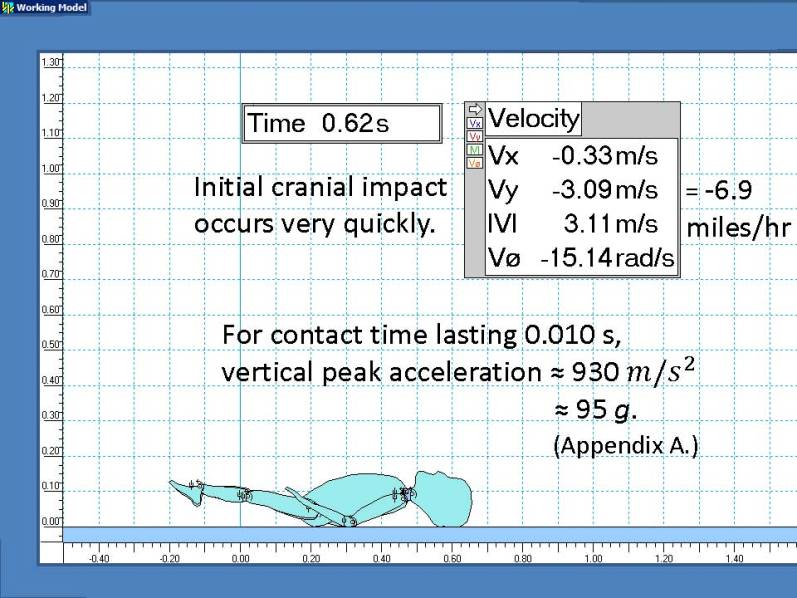
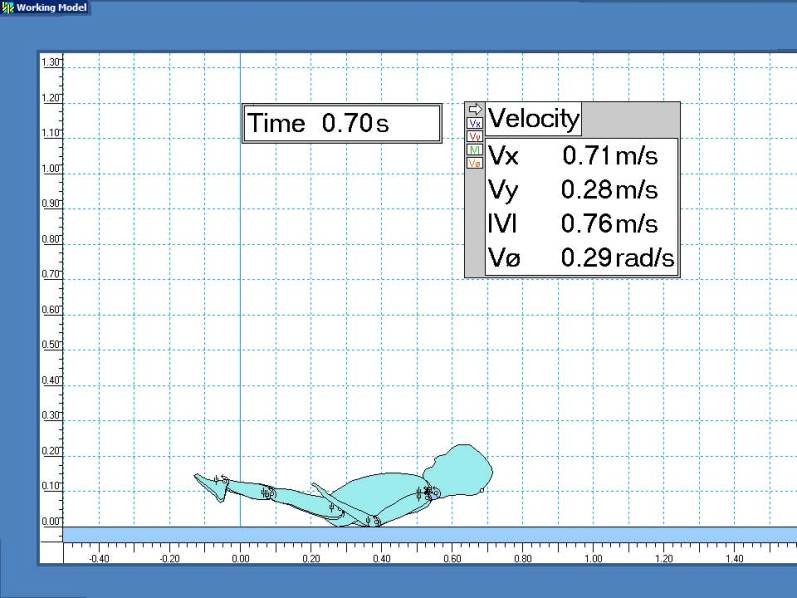
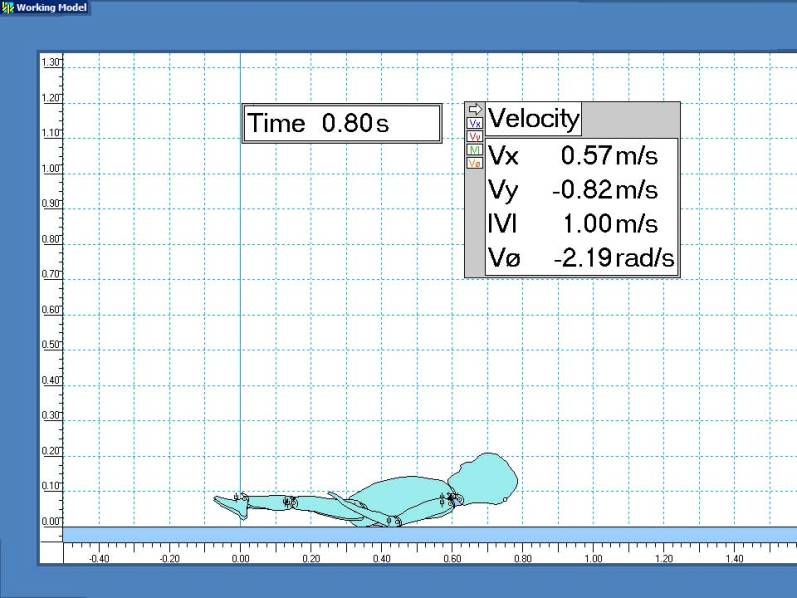
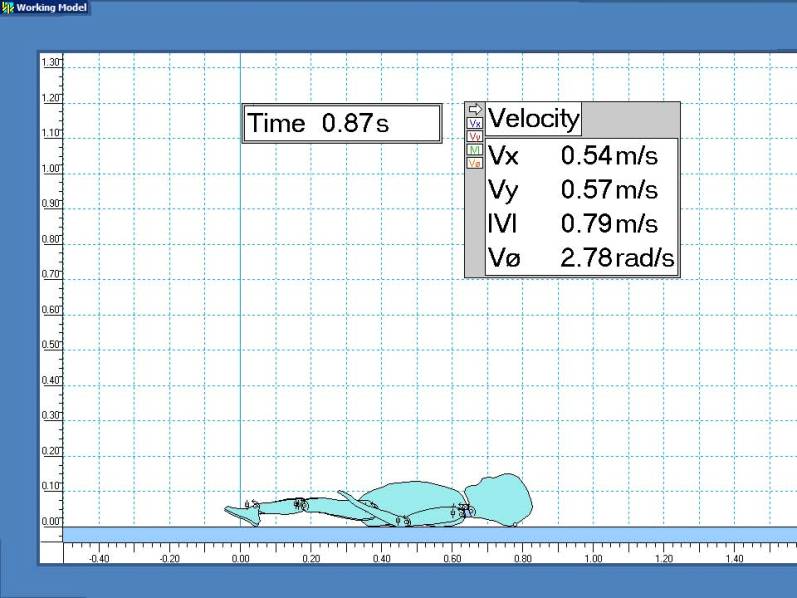
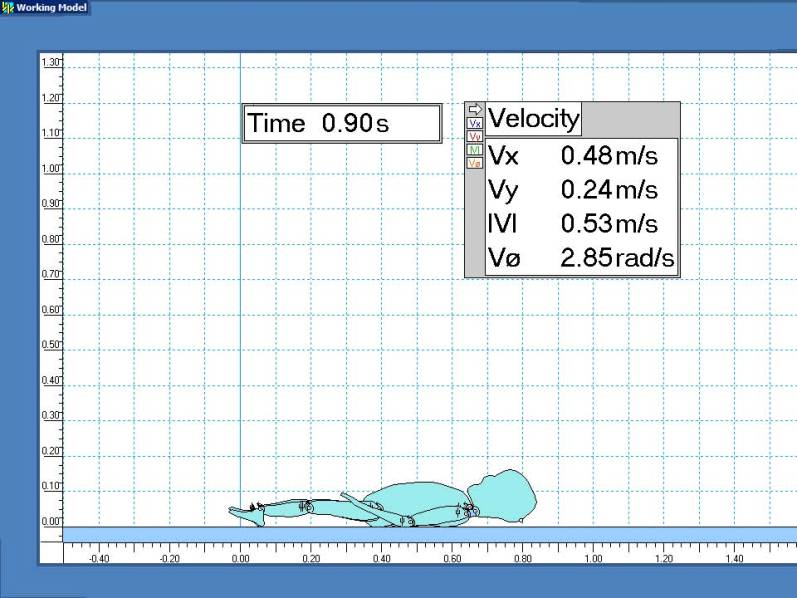
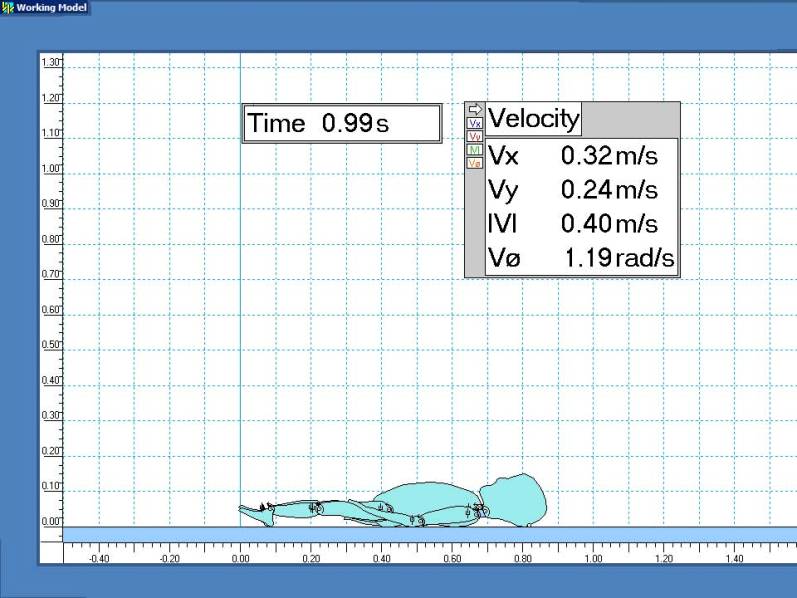
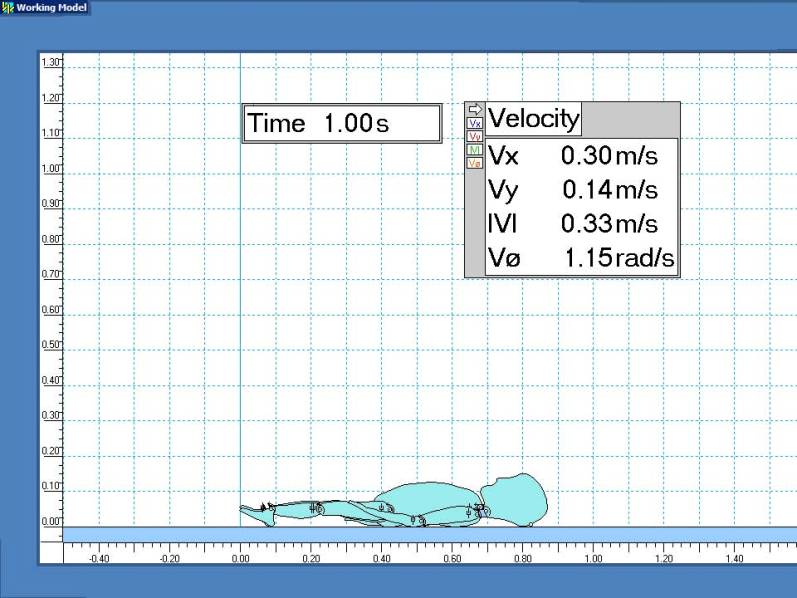
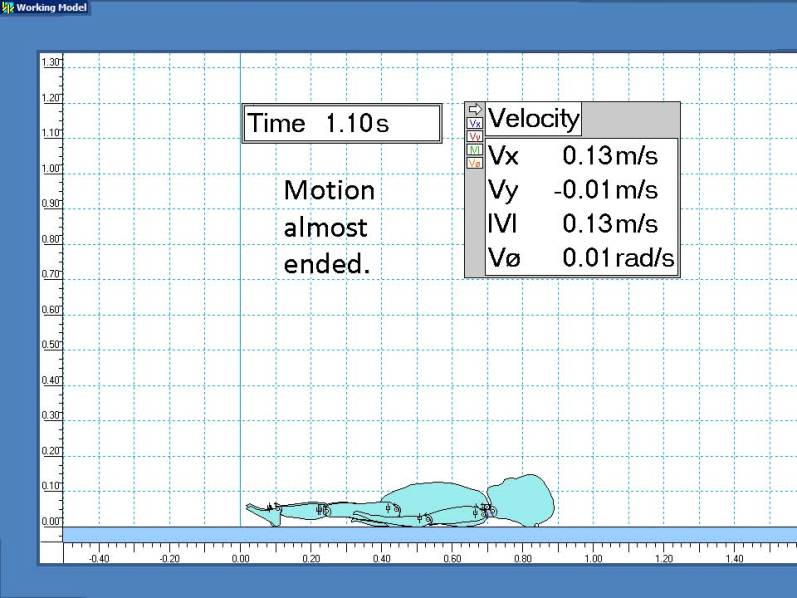
Conclusion
This simulation clearly shows the potential for severe head injuries from low-level falls.
The resulting accelerations and forces for the first impact are almost 10 times greater than those that can usually be produced by manually shaking a realistic dummy [3],[4].
Appendix A. Physics Relationships
By definition, the average acceleration in the vertical dimension ay = delta vy / Delta t
where delta vy is the change in velocity and Delta t is the interaction time with the floor.
A toddler head colliding with a rigid surface has Delta t aprox. 0.005 s [3],[4]. Moderate padding extends this to Delta t aprox 0.020 s. Delta t = 0.010 s was chosen as a typical value.
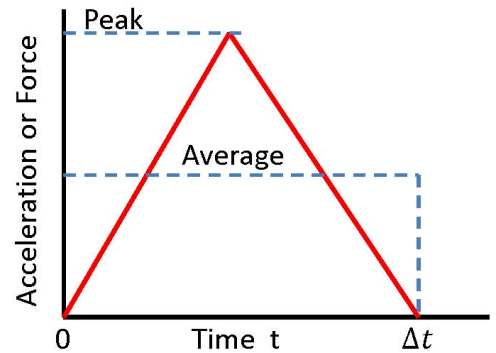
As illustrated, a linear approximation of the acceleration or force between the floor and the head shows that the maximum or peak value is about twice the average [4],[5].
Divide accelerations in m/s² by g = 9.8 m/s² to convert into g’s. Multiply accelerations by mass to convert into forces.
Appendix B. Model specifications for a typical 18 month old toddler [2]
By definition, elasticity or coefficient of restitution is modulus of rebound velocity / impact velocity. The head, arms, feet and floor are assigned values of 0.5, while the other segments are 0.1.
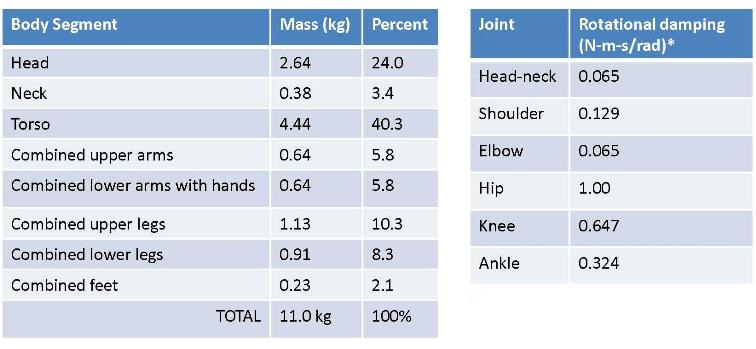
[*] Rotational damping values are chosen for realistic response since standards are impossible for a variable organism.
The coefficient of static friction = 0.30 foer everything but the feet, which = 0.90 for rubber soles.
The coefficient of kinetic friction = 0.20 for everything but the feet, which = 0.80 for rubber soles.
Kutta-Merson with 0.0001 second integration step provides accuracy and model stability. Every tenth step is illustrated.
References
[1] Baker, Susan P., O'Neill, Brian, Ginsburg, Marvin J., and Li, Guohua. The Injury Fact Book (Oxford University Press 1992), 2nd ed., p.140
[2] www.humaneticsatd.com/crash-test-dummies/children
[3] Ommaya A K, Goldsmith W and Thibault L. Biomechanics and neuropathology of adult and paediatric head injury. British Journal of Neurosurgery 2002; 16(3): 220-242
[4] Goldsmith W and Plunkett J. A biomechanical analysis of the causes of traumatic brain injury in infants and children. The American Journal of Forensic Medicine and Pathology June 2004; 25(2): 89-100
[5] Cross, Rod. The Bounce of a Ball. American Journal of Physics March 1999; 67 (3): 222-227
Per ulteriori informazioni contattare la Lista Studio srl®
OTHER 83 DIFFERENT APPLICATIONS !
ALTRI 83 CASI IN SETTORI DIVERSI !






















