A computer aided graphical synthesis was undertaken to understand the kinematics of a nose wheel landing gear mechanism such as that on the Lockheed F-16 using Working Model software. The mobility of the design was verified by computer animation.

To contrast the nose gear kinematic simulation, the main landing gear located under the wing of a light weight aircraft such as the Berkut (Ber-koot) was also studied. The Berkut is the product of Experimental Aviation, Inc. (E.A.I) located in Santa Monica, California. This plane was selected because it is representative of the growing market of kit and light weight general aviation aircraft in the 1,000 to 2,000 pound weight range. In this weight class, the Solid-Spring landing gear can be used instead of the oleoshock-strut type used in the F-16.

Computer modeling and finite element analysis are explored to analyze stresses developed while landing at normal sink rates.

The deflections of the main spring gear are calculated and the internal stresses evaluated utilizing the finite element program Stardyne (Research Engineers, Inc.). The results of the modeling and simulation are discussed in this paper.

Mechanism kinematics is a very important area in the design of aircraft landing gear. Gear design largely deals with links that make up the geometry of the landing gear and their spatial relationships. The geometry and kinematics of the gear are functions of the aircraft using the gear. Very seldom can any one kinematic design be used for several different aircraft since the design is a function of the individual aircraft’s need, i.e., weight, space, volume, aircraft’s mission, such as fighter, transport passenger, cargo, etc. Also of importance in the design of aircraft landing gear is the structure. The gear must be able to withstand the shocks of landing and taxiing. A collapse of a landing gear during the landing roll can have devastating effects on the aircraft. This paper seeks to investigate the methods used in the design of landing gear, with an introduction to the kinematics of landing gear design and a detailed structural analyses of a light weight 2000 lb aircraft’s main gear.

In this paper two analysis were performed. The first was the kinematic evaluation of a front nose gear such as the Lockheed F-16. The second analysis was a structural study of a main gear for a light weight aircraft such as the Berkut (see figure 3 and 4). The contrasting aircraft and their gears were chosen because, the F-16 nose gear typified the use of landing gear which needed to be retracted in tight spaces and showed economical use of linkages. On the other hand, the Berkut with it’s simple leaf spring gear was a good starting point for the evaluation of landing gear using hand and finite element computer analysis. Solid elements were used for this analysis. The theory for finite element method is complex and will not be explained here, nor will the theory of kinematics be explained, rather the procedures used to create the models will be discussed along with some of the decisions that were made in creating the models.

The first analysis was performed to understand the F-16 front gear (see Figure 1). The gear was modeled using stick diagrams based on dimensions furnished by Lockheed Martin Tactical Aircraft Systems (Puttman, 1995).

Stick diagrams serve a purpose similar to that of the electrical schematic or circuit diagram, in that they display only the essential skeleton of the mechanism which however embodies the key dimensions that determine the path of the motion. In the case of this analysis, the stick diagram was taken a step further. Basic geometry was drawn to represent the components of the F-16’s landing gear, then a kinematic simulation was performed using the student version of Working Model (Knowledge Revolution, 1995), a computer assisted design program that shows the motion in real-time.

Working Model is an advanced motion simulation package with sophisticated editing capabilities. The program makes it possible to build and analyze dynamic mechanical systems with essentially no programming. The software allows one to design, test, redesign and retest without building a physical model. The windows interface is intuitive and easy to learn. The dynamics engine is physics-based and enables the program to accurately calculate the behavior of even highly complex models.

The general methodology was to use a two dimensional four bar linkage technique for the computer analysis. Iteration produced a design which moved smoothly and freely. Results from the animation are shown in Figures 2a-2e.

The second analysis was the evaluation of the Berkut main landing gear (Figures 3-4). The first step was to draw a model of the landing gear strut in a CAD program from the dimensions supplied by Experimental Aviation, the manufacturer of the Berkut kit (Cox, 1991).

The next step was to calculate the maximum bending stress. This was necessary to validate the finite element results. The detailed finite element analysis results are only as good as the input data; hence the validation. The following data are employed in the Maple V calculations:

Shear Modulus, G = 4,000,000

Poisson’s Ratio, 0.33

Mass Density = 2.59062 x 10^-4

These "hand" calculations in Maple follow Pazmany (1986) one of the few sources for light aircraft landing gear design available.

The Maple calculations and results:

Section Modulus required at root: I_x/y = BM

BM (Bending Moment) comes from the fact that the aircraft’s deceleration load is 3453 lb and the strut length is 42 inches

BM/Fby;

2.756234792

Actual Section Modulus at Root is I_x/y = bh²/6:

Bending Stress at Root:

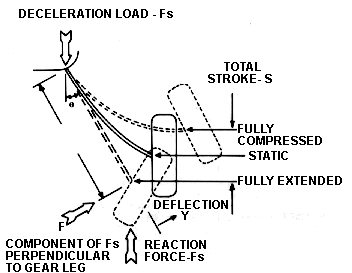
The next step was to calculate deflection. the criterion for deflection first comes from the deceleration load imposed on the strut (see figure 5).

The following calculations determined the deflection on the strut due to landing the aircraft.

FAA design conditions require each main wheel to carry a vertical load at least equal to the airplane gross weight per Federal Aviation Regulations (FAR) 23.473 (g) and FAR 23, Appendix C. This is equivalent to a 2 g impact load on the main wheel and strut. The following deflection formula will establish acceptable strut cross-section dimensions based upon calculations developed for the Berkut aircraft.

Aluminum leaf spring strut nomenclature.

D = strut deflection at the axle under 2 g impact load = ((W*l^3)/(3*E*i))*Sec(q )

W = Aircraft gross weight in pounds

S = wing area in square feet.

l = strut length in inches

TD = Tire Deflection

E = the modulus of elasticity

i = moment of inertia of the strut

q = strut angle from the vertical

Vd = descent velocity in ft/s

d =vertical stopping distance in feet at Vd=0

Note: according to Federal Aviation Regulations (FAR) 23.473 (d), the initial descent velocity for landing gear design calculations cannot be less than 4.4(W/S)^(1/4)

LVGDIF = landing gear vertical g design inertia factor

VDIF = vertical design inertia factor

h = inertia load factor

Note: FAR 23.73 (e) permits a load reduction of 0.67 g due to wing lift assumed to act during landing, so the landing gear design load factor (LDLF) = h - 0.67

Looking at the formula it appears that the moment of inertia "i" holds the key to adequate deflection of the strut under impact load conditions. If "i" is too large, the deflection is too low and the impact load factor is high; in other words, the gear is too stiff. The following calculations show the effect of deflection on the design load factor. When developing a strut design it is necessary to vary strut dimensions b and h until sufficient deflection is obtained to provide acceptable vertical load factors, and hopefully without a too soft or "springy" gear.

The Maple V version 4 code (with results) for deflection and stress calculations follow:

The final step was to take the CAD model of the landing gear and enter it into the Stardyne finite element modeling program for auto meshing and static and dynamic analysis. The version of Stardyne used was very full featured and relatively easy to use for a cost $3900. The output is in the Appendix.

An additional simulation of the dynamics of the Berkut landing gear was attempted using Working Model version 2. In general, Working Model cannot model flexible bodies. However, Working Model can accurately simulate the motion of flexible beams by dividing the beam into discrete segments joined by springs with carefully chosen spring constants (Reckdahl, 1995). Unfortunately, because of the method of numeric integration employed in version 2 extremely long calculation times precluded obtaining simulations. Real-time simulations of the deflection of the landing gear were obtained using unrealistic parameters which are not discussed here. The most recent version of Working Model is reported to have improved numerical integration algorithms.

The computer analysis of the F-16 synthesized a nose gear, which consisted of a shock strut, a two part drag brace and a single actuator. The dimensions for the simulated landing gear were taken from data supplied by Lockheed. Upon trying to replicate this gear, there was binding in two linkages that made up the drag brace. This problem was resolved by making small modifications to the geometry to make up for the 3-dimensional character of the actual gear which could not be reproduced with the 2-D version 2 of Working Model. The simulation was repeatedly rerun resulting eventually in smooth relative motion.

For the Berkut aircraft, "hand" calculations were performed for the bending stress using Maple V. The results from the calculations showed that there would be highest bending stress at the root of the strut which is the top of the strut that attaches to the aircraft. The calculated stress was 86,309 psi, which exceeds the yield stress (42,000 psi ) of the aluminum material. The results of the finite element analysis were close to the Maple V calculations with a peak stress of 89,376 psi, (see Figure 7) with an average stress of 57,784 psi (see Figure 6). From the finite element analysis it appears that the stress is distributed longitudinally up the strut (see Figure 8). The maximum stress seems to be located in only a small portion of the top side corner of the root of the strut (see Figure 9). In addition to the bending stress, the Maple V calculations also showed that there would be a deflection of 6.008 inches for the landing gear and a landing gear design load factor of 2.05 g. The actual Berkut uses stronger carbon fiber reinforced plastic composite material for the landing gear. Nearly all details of the construction of the gear are considered proprietary information by Experimental Aviation, Inc. An attempt to model the gear using carbon composite material was unsuccessful. While the Stardyne code is advertised to allow up to 45 plies of composite material, we were unable to get the program to accept more than 27 which was insufficient to model the gear.

Working Model software improves education for students by providing an easily constructed simulation of the behavior of the motion of the linkage comprising a front landing gear. It is difficult to visualize and analyze the retraction and extension processes and their relationship to component geometry in landing gear kinematics. The software makes it very easy evaluate velocity, acceleration and force quantitatively for a design by adding numeric or graphical output meters. The interface is graphic and intuitive.

The Stardyne finite element software allows the student to see the deflected shape of the maximally loaded Berkut main landing gear. It also provides the student a pictorial output for stress levels corresponding to the gear geometry analyzed. Here it is evident that high stress levels occurred in a very small area. The gear design should avoid sharp angles in this area, substituting smooth curves with radii big enough to reduce stress concentration. The deflection for the gear, even using aluminum material, satisfies the requirements set by FAR 23 for a 2g landing load.

MAXIMUM STRESS SUMMARY FOR CUBES LOAD CASE NO.

MAXIMUM PRINCIPAL STRESS = 0.3902530E+05 IN CUBE NO 1865

MINIMUM PRINCIPAL STRESS = -0.6683470E+05 IN CUBE NO 1782

MAXIMUM SHEAR STRESS = 0.5145041E+05 IN CUBE NO 1782

MAXIMUM VONMISES VALUE = 0.8937632E+05 IN CUBE NO 1782

Derek is a senior MET student at Purdue University Calumet and a McNair scholar. He formerly worked for IBM. He has presented three papers at the ASEE Illinois-Indiana Section meeting.